介绍
KMP 算法是一个比较经典的字符串匹配算法,最简单的匹配算法是 Brute-Force 算法,即纯暴力算法。纯暴力算法的思路很简单,比对模式串和主串每个字符,遇到不匹配的就将模式串往主串往后移动一位再此进行比对,以此往后,直到模式串全部比对成功
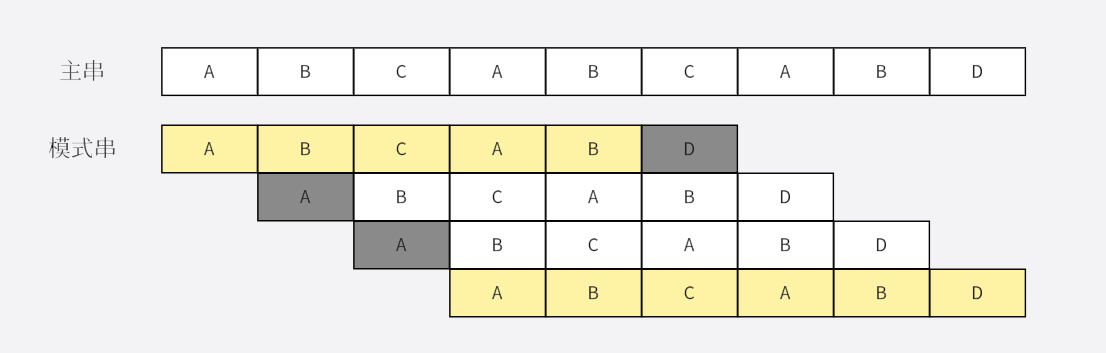
Brute-Force 算法
而 KMP 算法是根据纯暴力算法提出的一种改进算法。从纯暴力算法可以看出它其实对已经比对部分的信息利用很少,在第一次比对时我们就已经知道前5个字符是完全一样的,而前5个字符中模式串的第1、2两个字符和第4、5两个字符一样,进行下一次比对的时候完全可以直接将模式串移动到主串第4个字符处。
KMP 根据这种信息提出了部分匹配值用来实现这种快速移动,部分匹配值其实就是记录了当前匹配的模式串部分最前部分和尾部是有多少是相同的,也就是上面的"AB",然后根据这个值通过如下计算方式来跳转模式串匹配位置。
主串位置 + 模式串已经匹配的部分 - 部分匹配值其实这个公式也比较好理解,先假设已经匹配的部分不用再匹配了,直接跳转到未匹配的主串位置,然后再看看已经匹配部分的末尾有没有和模式串头部一样的部分,有的话则往前移动。
部分匹配值的计算方法也比较简单,就是找寻前缀和后缀共有元素的长度,前缀即去掉最后一个字符剩下字符的全部头部组合,后缀即去掉第一个字符全部尾部组合,这里以“ABCABC”为例来计算部分匹配值
"A":前缀为空,后缀为空,共有元素长度为0
"AB":前缀为{A},后缀为{B},共有元素长度为0
"ABC":前缀为{A, AB},后缀为{BC, C},共有元素长度为0
"ABCA":前缀为{A, AB, ABC},后缀为{BCA, CA, A},共有元素为A长度为1
"ABCAB":前缀为{A, AB, ABC, ABCA},后缀为{BCAB, CAB, AB, B},共有元素AB长度为2
"ABCABD":前缀为{A, AB, ABC, ABCA, ABCAB},后缀为{BCABD, CABD, ABD, BD, D},共有元素长度为0| A | B | C | A | B | D |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 2 | 0 |
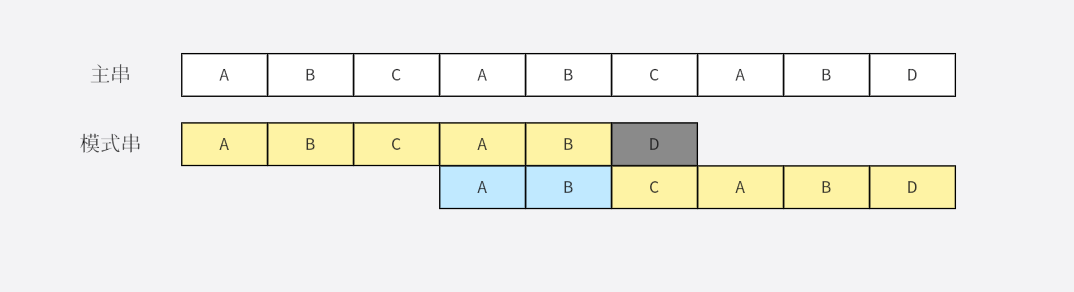
KMP 算法
Rust 实现
fn get_pattern_match(s: &str) -> usize {
for i in (0..s.len()).rev() {
let prefix = &s[0..i];
let suffix = &s[s.len() - i..];
if prefix == suffix {
return i;
}
}
return 0;
}
fn get_nxt(s: &str) -> Vec<usize> {
let mut v: Vec<usize> = vec![0; s.len()];
for i in 0..s.len() {
v[i] = get_pattern_match(&s[0..=i]);
}
return v;
}
fn search(s: &str, m: &str, v: &Vec<usize>) -> usize {
let mut n = 0;
while n < s.len() {
for i in 0..=m.len() {
if i == m.len() { // 如果i达到和模式串一样长度则说明完全匹配
return n;
}
let p1 = &s[n..=n + i];
let p2 = &m[0..=i];
if p1 != p2 {
if i == 0 { // 如果第一个字符就匹配不上,默认加1
n += 1;
break;
}
n += i - v[i-1]; // 这里的i指向的是失败的索引,对应的nxt中要将i-1
break;
}
}
}
return 0;
}
fn main() {
let s = "abcabcabd";
let m = "abcabd";
let v = get_nxt(m);
let i = search(s, m, &v);
println!("{}", i);
}